E.3.  Inefficient spend consumed immediately

The EPP can be represented by a 'stock' of future expenditure aggregated from all the component projects within it, as shown in Figure E-1a. In-year expenditure (to meet "control total") represents an outflow from stock. Additions to the EPP in any year (less any cancellations) are an inflow to stock. These amounts are lumpy, but in the first instance need to average to around the level of outflows otherwise the stock level will build.

Supposing that the amount of productive spend required by the EPP at time t is given by p(t), an amount of cost a(t) is added to the EPP over time, and that, in total, the amount spent on the EPP is s(t). Assuming that unproductive spend that arises from delay is consumed immediately and forms part of that period's expenditure, then s(t) can be split into efficient spend, sp(t), and inefficient spend, sq(t), which arises at a rate proportional to p(t), with a constant coefficient, β.

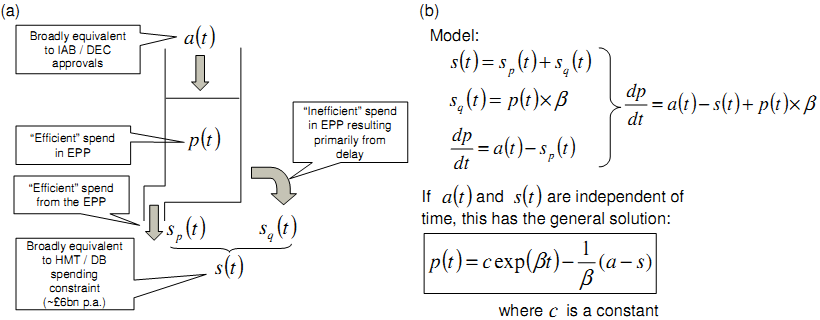
Figure E-1 : (a) Diagram of simple conceptual model of the equipment plan with inefficient spend consumed immediately; (b) Equations that govern the model. Descriptions of the main variables can be found in the text; constant c is defined by starting conditions.

It is possible to express the model in terms of equations that govern the relationship between the differing amounts of spend, the value of projects added to the EPP, and the value of the 'efficient' spend in the EPP. As shown in Figure E-1b, these equations can be solved generally and illustrate the exponential nature of the value of the EPP. In particular, in the circumstance when total spend s(t) is constrained (e.g., for budgetary purposes), the amount of 'efficient' spend resulting from the EPP shrinks at an exponential rate as more of the spend has to be committed to generating 'inefficient' output.