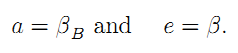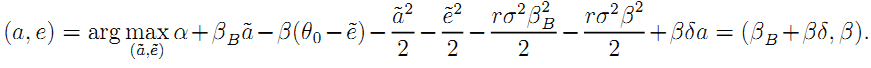3.2.2 Quality Incentives

Let us now suppose that a noisy index q of the quality of the infrastructure is available:

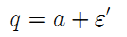
where ε' is a random variable which is assumed to be normally distributed with variance 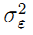and zero mean. For simplicity we keep the same variance of noise on q and the operating costs. This assumption is particularly relevant for the case where q is in fact an earlier realization of operating costs in a context where the investment consists of complementary and renewed assets.

Now the builder's incentive scheme links his reward to the realized level of q. For simplicity, we assume again that such contracts are of the form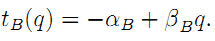

Unbundling: Incentive constraints for the builder and the operator are given by:

Intuitively, although the ability to write complete contracts on a quality index improves the builder's incentives and raises the quality of the infrastructure, it does not change the operator's incentives. As a result, the second-best effort remains unchanged.

Bundling: The consortium's incentive constraint can be written as:

By making F's payment depend on the quality index, G gives to F more incentives to invest in asset quality. As F is risk-averse such contingent payment raises the risk premium by However, under bundling and a positive externality, part of the risk necessary to induce incentives in quality-enhancing can be obtained by making the cost reimbursement rule more powerful without undermining operational costs. This reduces the risk-premium related to the design activity and improves welfare.

Result 4 Bundling strictly dominates unbundling when complete contracts on both operating costs and a quality index are feasible and the externality is positive.

Even if better information over asset quality eases the agency problem under un-bundling, bundling remains the preferred option whenever the auditing of infrastructure quality is imperfect.