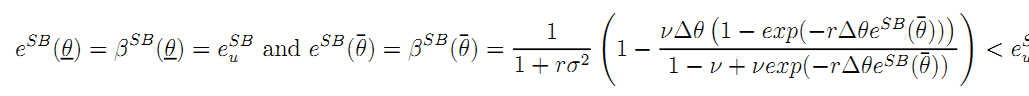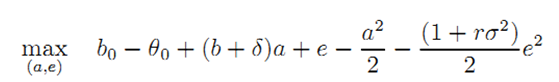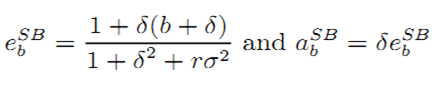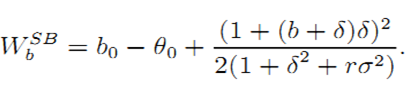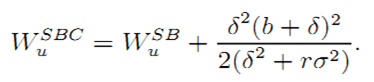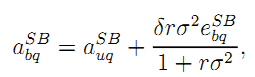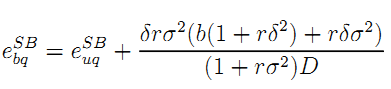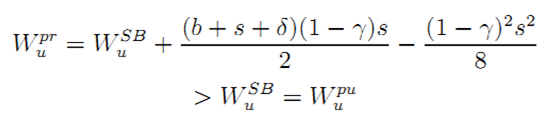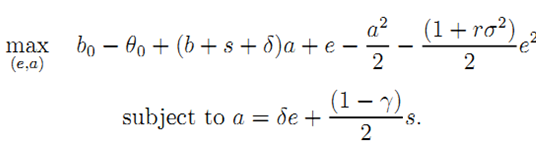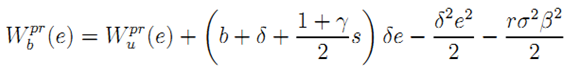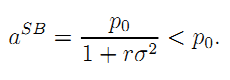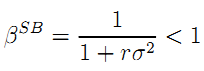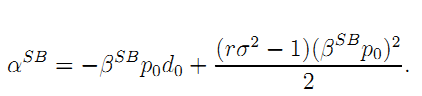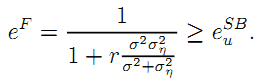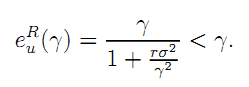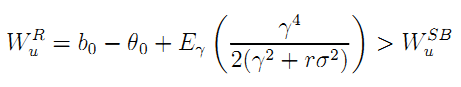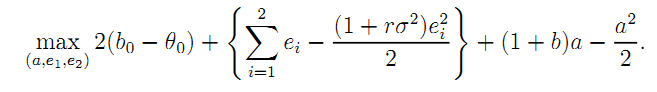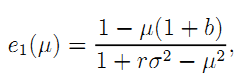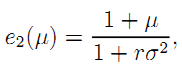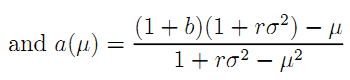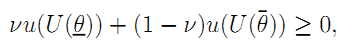Appendix
• Proof of Result 2: Aggregating the two relevant incentive constraints in (6) by eliminating the slope of the incentive scheme β yields the following expression of G's problem:
| (A.1) |
subject to a = δe.
Optimizing yields the effort levels
| (A.2) |
and the expression of the expected welfare as:
| (A.3) |
The comparative statics results on WbSB and WuSB immediately follow.
The exact expressions for efforts under bundling are
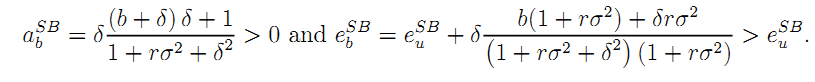
Note that ebSB may be greater than ebFB if b is large enough. For ebSB ≤ eFB, we need
δb ≤ rσ2.

• Proof of Result 3: Equation (7) yields the following expression of the expected welfare with complete contracts and unbundling:
| (A.4) |
It is easily seen that the gain from writing complete contracts compared with the setting of Section 3.1 is of order δ2 which is rather small for a weak externality.
When bundling is chosen, a single incentive scheme must incentivize both dimensions of effort. The outcome is the same as in Section 3.1 and WbSBC = WbSB. Up to terms of order at least δ2, (A.3) can be approximated when δ is small enough as:
The result follows. 
• Proof of Result 4: Consider first the case of unbundling with the incentive constraints (8). Taking into account the risk-premium involved when contracting with the builder and the operator, G's optimization problem becomes:
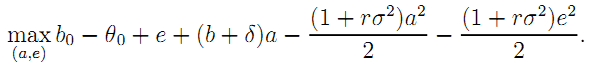
Optimization leads to:
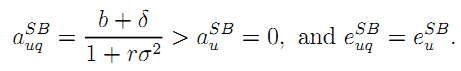
Consider now the case of bundling taking into account the incentive constraint (23). Since G has all bargaining power in designing the consortium's contract and extracts all its ex ante surplus, G's optimization problem becomes:
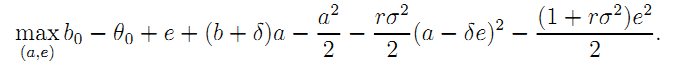
The maximand above is greater than under unbundling for a positive externality. The reverse holds for a negative externality.
The optimal effort levels are given by:
|
|
|
where D = (1 + rσ2)2 + rδ2σ2. It is immediate to check that
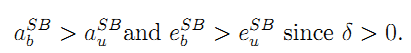

• Proof of Results 5 and 6: Under private ownership and unbundling, G can extract all the owner's surplus through an ex ante fee because he has all bargaining power exante. Given the effort levels defined in (10) and (11), we get the following expression of social welfare:
| (A.5) |
so that Result 5 holds.
Under private ownership and bundling, ownership has still some value. Taking into account the incentive constraint (12), observing that G extracts now all ex ante surplus from the consortium by raising the fixed-fee α by an amount that covers the extra net benefit that the owner can withdraw from his investment, and finally, aggregating the two incentive constraints in (12), we obtain the following expression of G's maximization problem:
| (A.6) |
We use (A.6) to express G's objective function under unbundling and private ownership before optimization with respect to e as:
| (A.7) |
where
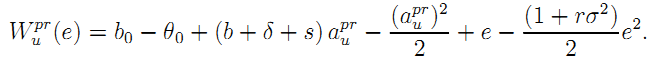
The result immediately follows. 
• Proof of Result 7: Taking into account that the government can extract all profit from the firm, the government's problem becomes now:
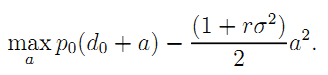
Immediate optimization yields the second-best value of the operating effort as:
| (A.8) |
Note that p0 is the first-best level of effort that the firm would implement under risk-neutrality since it could then be made residual claimant for the whole benefit of any revenue-enhancing effort.
To implement the second-best level of effort, the government designs a contract with the following features:
|
|
|
The result then follows. 
• Proof of Result 8: The social welfare maximizing government is concerned by the social value of the project over its entire life. This gives us the following expression of the government's problem:
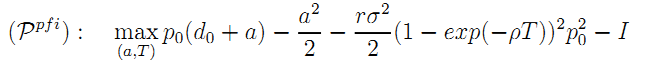
subject to (14) and (15).
Suppose first that the investment constraint (15) is slack. The second-best effort level is then easily obtained as (16), from which, we derive the optimal unconstrained length of the franchise as (17). Suppose that TSB is such that (15) does not hold, i.e.,
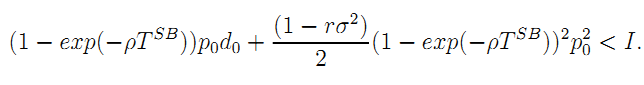
The new duration of the contract must solve:
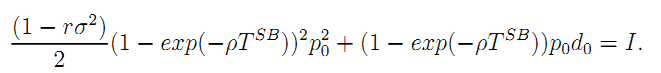
Assuming that 1 > rσ2, we immediately derive the expression of the incentive intensity
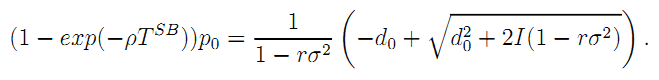
This formula yields the comparative static results of Result 8. 
• Proof of Result 9: Taking into account the risk-premium borne by the firm and the coalitional incentive constraint (21), we obtain the following expression of the government's problem:
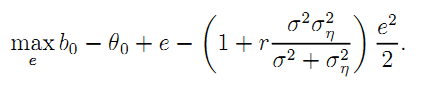
It is straightforward to derive the optimal effort as
| (A.9) |

• Proof of Result 10: Consider the case of bundling. The realized expected welfare is still given by (A.7). In particular, when δ is small, we know that WbSB - WSB is of order δ.
Consider now the case of unbundling. The optimal effort depends now on 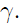 Easy computations yield:
Easy computations yield:
| (A.10) |
The expected welfare becomes:
| (A.11) |
where the last inequality follows from Jensen inequality and the fact that 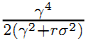 is convex in
is convex in 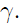 Note that WUR differs from WuSB by a term of order zero in δ.
Note that WUR differs from WuSB by a term of order zero in δ. 
• Proof of Result 11: G has still all bargaining power in designing the firm's contractand uses accordingly the intertemporal fixed-fee α1 + α2 to extract all ex ante surplus from the firm. Aggregating the three incentive constraints (22) into a single one, G's optimization problem becomes:
| (A.12) |
subject to e2 = ae1.
Denote by µ the multiplier of (A.12). Observe that the first-order conditions w.r.t. (e1, e2, a) can be written respectively as:
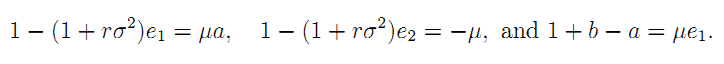
From this, we can express (e1, e2, a) as functions of µ:
|
|
|
which are all positive effort levels when 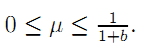
Inserting into (A. 12), we get that µ solves:
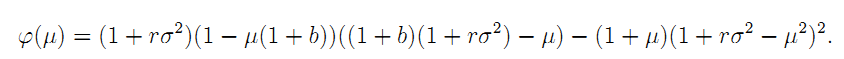
Note that 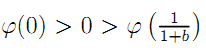 so that the latter equation has a root
so that the latter equation has a root 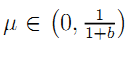 , which yields the result.
, which yields the result.
• Proof of Result 12: Contracting taking place ex ante, i.e., before the firm learns its innate costs, the following ex ante participation constraint must hold:
| (A.13) |
where the firm's Von Neuman-Morgenstern utility is 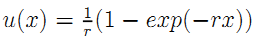 because of constant risk-aversion.
because of constant risk-aversion.
Being given the social benefit b0 of the project, the government's problem can now be written as:
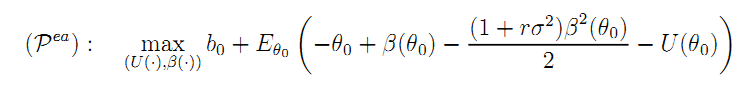
subject to (26) and (A.13).
Observing that both (26) and (A.13) are binding yields the following expressions of the certainty equivalent for the firm's payoff for each realization of θ0 as:
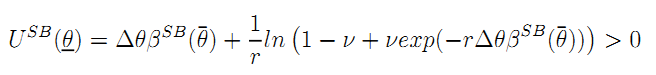
and
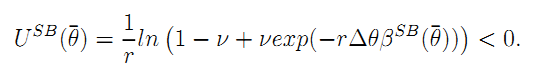
The levels of effort are respectively given by: