2. Calculation of Internal Rate of Return Using Linear Interpolation
Note that this simple example calculates an APPROXIMATION of the Internal Rate of Return using a mathematical method called "Linear Interpolation". In order to make this approximation, it is necessary to make two Net Present Value calculations. One of these calculations MUST give an NPV which is positive, and the other calculation MUST give an NPV which is negative. The subsequent process of linear interpolation then uses these two NPVs (one positive and one negative) to estimate the point (or, more correctly, the interest rate) at which the NPV is exactly zero. This point will be the Internal Rate of Return (IRR). Note that the "Discount Factors" are calculated using the following formula: discount factor in year n = (l + r)-n
where r = interest rate (e.g. 0.1 for 10%) and n = year.
|
|
| @10% p.a. | @15% p.a. | ||
| Year | Future Value | Discount Factor | Present Value | Discount Factor | Present Value |
| Net | (£) |
| (£) |
| (£) |
| Year 0 | (20,000)4 | 1.0000 | (20,000) | 1.0000 | (20,000) |
| Year 1 | 2,000 | 0.9091 | 1,818 | 0.8696 | 1,739 |
| Year 2 | 4,000 | 0.8264 | 3,306 | 0.7561 | 3,024 |
| Year 3 | 6,000 | 0.7513 | 4,508 | 0.6575 | 3,945 |
| Year 4 | 8,000 | 0.6830 | 5,464 | 0.5718 | 4,574 |
| Year 5 | 10,000 | 0.6209 | 6,209 | 0.4972 | 4,972 |
|
|
| 1,305 |
| (1,746) | |
In this example the IRR is calculated as follows:
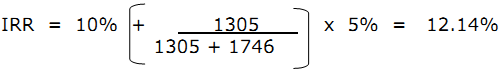
The graphical solution is shown in Figure 1.
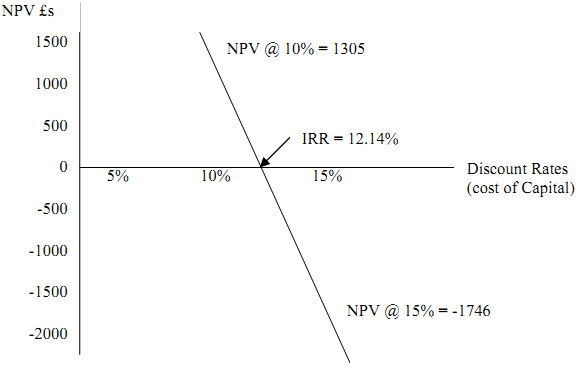
Figure 1 - graphical representation of IRR calculation
Problems of Using Linear Interpolation For Estimating IRR
In using Linear Interpolation for estimating the IRR, we have assumed a linear relationship between interest rates and NPV. In fact, the relationship is NOT linear. If we were to calculate the NPVs for the project using a large number of interest rates and then plot these NPVs on a graph, we would produce a curve. The relationship is, in fact, curvilinear. Thus, by using linear interpolation to estimate IRR, we have taken a short-cut across the curve, with the result that the estimate of IRR is slightly too high. In the above calculation, we have used interest rates of 10 % p.a. and 15 % p.a. - a range of 5 %. Had we used a larger range (say, by using interest rates of 9 % p.a. and 16 % p.a. - a range of 7 %), the effect of the "short-cut" would have been greater and the error in estimating the IRR would, thus, be greater. In practice, so long as the range of interest rates selected is not too high, the above method of estimating IRR is sufficiently accurate for most purposes. In practice, a computer program or a programmable calculator would eliminate this estimation error.
________________________________________________________________________
4 Figures in brackets represent negative figures.