Survival Time Maximum Likelihood Estimation

It is natural to adopt a nonparametric model in cases where the functional form of the hazard model is unknown. In general, however, letting data inform the functional form is also desirable since deciding the form of the hazard function is itself an empirical question.

PPP projects are at risk from socio-macroeconomic and project-based factors. Using Nose's (2014) contract framework, the hazard model is applied to determine the probability of a project failing over the contract duration. This is denoted as Ai, measured by the number of years from the financial closure year (t0) to the year that the project was cancelled or declared in distress ti :

The active projects were still ongoing in 2015 and classified as right-censored, since their duration was not completed up to that point (the censoring time is denoted as c, which is the same for all contracts). If the duration is not censored, the density of Ai is simply f (Ai | xi; θ)and the probability of Ai is censored if , and therefore the maximum likelihood estimate θ of can be obtained by maximizing the following log-likelihood function:

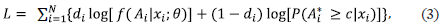
where di is a censoring indicator. The covariates of project i in sector j in country c are represented by xi = [X_1,i, X2,c k, Dj]. The X1,i are project-specific characteristics, including direct and indirect government support, procurement type, MDB involvement, share of private investment in the contract, proposal mode, and type of PTP.

Macroeconomic conditions, X2,C, include indicators that may affect PPP project operations, such as growth, trade openness, terms of trade, and political and institutional factors, including a country's corruption and investment profile. The impact of natural disasters is also included, as some empirical findings recognize their effect on the growth of countries at different levels of economic development (Alano and Lee 2016), which can cause an increase in political conflict (Miguel, Satyanath, and Sergenti 2004). The regional fixed effects K and a vector of dummies for sectoral affiliations Dj need to be included in the likelihood function.

The hazard function λ can be estimated with maximum likelihood estimation,, following a Weibull distribution:2

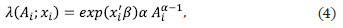
where a is the measure of duration dependence.